Inscriptionism
 |
| Inscriptional Model |
These aren’t just physical characteristics; they’re universal truths encoded into the very nature of what it means to be a circle.
The Circle as an Inscribed Entity
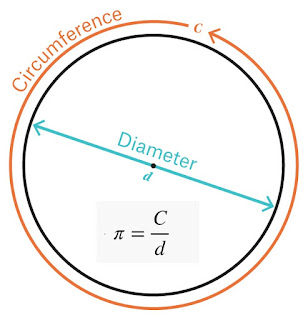
Radius (r)
Diameter (2r)
Circumference (2πr)
Area (πr²)
π (pi)—a constant that transcends size or material
No matter if it’s the orbit of a planet or the outline of a coin, the relational structure stays the same. It’s as if “circle-ness” comes with a built-in instruction set, waiting to be expressed in the real world.
In Lawsin’s terms, these aren't just mathematical descriptions—they could be seen as inscriptive codes:
The identity of the circle is preloaded with these embedded parameters.
The moment an object satisfies those inscriptions, it manifests as a circle—regardless of scale, substance, or intention.
Inherent properties act like inscriptions, determining how an entity behaves or appears across contexts.
That raises a deep question: if shapes like circles carry inscriptions, could the laws of physics themselves be a grand inscription on the universe?
Atomic Inscriptions: The Built-In Behavioral Blueprint
Every element in the periodic table has a set of internal “codes”:
Electron configuration: Determines how it bonds.
Valence electrons: Define reactivity and preferred partners.
Electronegativity: Drives attraction between atoms.
Energy states & orbitals: Dictate how atoms share or transfer electrons.
These are not optional traits—they're immutable inscriptions written into the identity of the element.
The Dance of Carbon and Oxygen
When carbon (C) and oxygen (O) meet:
Their inscriptions line up: oxygen is highly electronegative, carbon is eager to share electrons.
Under the right conditions (heat, pressure, catalysts), their “chemical compatibility” activates.
They form molecules like CO₂, releasing energy—almost as if obeying a script embedded in their atomic code.
It's not random—it’s an inevitable performance when the right players meet on the right stage.
Lawsin’s Scientific Theory of Everything isn’t just about physics or biology—it’s a unified model that attempts to explain existence, consciousness, and life through the lens of inscriptions:
Everything that exists carries embedded instructions—like atoms, shapes, or even thoughts.
These inscriptions are not symbolic, but functional—they guide how things behave, interact, and evolve.
STOE proposes that matter and energy are not enough to explain life; information (inscriptions) is the missing piece.
The “Bundle of Entities” Principle
Lawsin proposes that:
No single entity can exist truly on its own.
Every thing—atom, object, concept—is part of a co-dependent system, where its identity and functionality arise from its relationships with other entities.
These bundles operate through inscriptions: built-in interactions, parameters, and rules that connect them.
For example:
A seed doesn't just exist as a standalone biological object—it comes bundled with DNA, moisture, sunlight, and chemical instructions that enable its transformation.
A circle, as you noted earlier, always comes with π, radius, perimeter, etc.—its existence is inherently multi-faceted.
In a way, it’s like a musical score:
The sheet music is the inscription—it defines the structure.
The orchestra and instruments, guided by STOE’s bundled dynamics, bring the composition to life.
So yes—without STOE’s activation model, inscriptions remain inert. It's the symphony of encoded potential meeting activating forces that turns a seed into a living, growing entity.
* existence is never a solo act, but a bundle of co-dependent forces
A circle, no matter how big or small, is self-contained:
Its form is defined by radius, circumference, and π.
Its function is to remain a circle—its inscriptions govern its behavior, but it doesn't spontaneously evolve into a square or a sphere. It expresses its nature perfectly—but only itself.
-------------------------------------------
Comments
Post a Comment